マクスウェル方程式積分形の意味と電磁場の関係

マクスウェル方程式積分形の意味

マクスウェル方程式積分形とは何か

 

マクスウェル方程式の積分形は、電磁場の振る舞いを大域的な量で表現した形式です。微分形が空間の各点における局所的な性質を記述するのに対し、積分形は閉曲面や閉曲線といった有限の領域全体での性質を表します。

 

参考）マクスウェル方程式の意味
​
4つの基本方程式は以下のように表されます。ガウスの法則では閉曲面を貫く電気力線の総数が内部の電荷量に比例すること、磁場に関するガウスの法則では磁気単極子が存在しないため磁束の流入と流出が等しいこと、ファラデーの電磁誘導の法則では磁束の時間変化が起電力を生むこと、アンペール・マクスウェルの法則では電流と電場の変化が磁場の循環を生むことを意味します。

 

参考）マクスウェルの方程式 - Wikipedia
​
積分形の最大の特徴は、物理的な意味が直感的に理解しやすい点にあります。例えばガウスの法則の積分形は「閉曲面を通る電場の総流束が、その内部の電荷を誘電率で割ったものに等しい」という明確な物理像を提供します。

 

参考）マクスウェル方程式
​

マクスウェル方程式積分形と微分形の変換

積分形と微分形は数学的に等価であり、ガウスの発散定理とストークスの定理を用いて相互に変換できます。ガウスの発散定理は体積積分と閉曲面の面積分を関連付け、ストークスの定理は面積分と閉曲線の線積分を結びつけます。

 

参考）マクスウェル方程式の積分形から微分形を導出する
​
微分形から積分形への導出では、まず微分形の両辺を適切な領域で積分します。例えばガウスの法則の微分形 ∇·E = ρ/ε₀ の両辺を体積積分し、左辺にガウスの発散定理を適用すると積分形が得られます。逆に積分形から微分形を導く際は、任意の領域で積分形が成立することを利用して被積分関数同士の等式を導きます。

 

参考）マクスウェル方程式の微分形と積分形 - MathWills
​
この変換関係により、問題の性質に応じて最適な形式を選択できます。対称性の高い問題では積分形が計算を簡略化し、一般的な境界条件を扱う場合は微分形が適しています。

 

参考）大学物理のフットノート
​

マクスウェル方程式積分形における電場と磁場

積分形における電場Eと磁場Bの関係は、電磁気現象の本質を表しています。電場の積分形では、閉曲面上での電場の法線成分を面積分することで、内部の電荷総量を求められます。これは電気力線が正電荷から出て負電荷に入るという性質を数式化したものです。

 

参考）Maxwell方程式の微分形と積分形
​
磁場については、閉曲面を貫く磁束の総和が常にゼロになります。これは磁気単極子(磁荷)が存在しないことを意味し、磁力線は必ず閉じた曲線を形成します。この性質は積分形で表すと ∮B·dS = 0 となり、磁束密度の面積分がゼロであることを示します。
​
ファラデーの電磁誘導の法則では、閉曲線に沿った電場の循環が磁束の時間変化率に等しくなります。この関係式は発電機の原理を表しており、磁場の変化が電場を生み出すメカニズムを記述します。

 

参考）マクスウェル方程式の積分表示（ストークスの定理関連） - 相…
​

マクスウェル方程式積分形の具体的な応用

積分形は対称性を持つ電磁場問題の計算で威力を発揮します。点電荷の周りの電場を求める場合、ガウスの法則の積分形を球対称性と組み合わせることで、容易に電場の強さを導出できます。無限に長い直線電流が作る磁場の計算では、アンペールの法則の積分形と円筒対称性を利用します。
​
電磁波の導出においても積分形が基礎となります。真空中のマクスウェル方程式から波動方程式を導く際、微分形を用いますが、その背後には積分形で表される物理的な意味があります。電場と磁場が互いに直交しながら伝播する電磁波の性質は、マクスウェル方程式の積分形が示す電磁場の相互作用から生まれます。

 

参考）真空中のマクスウェル方程式と波動方程式 - 光学技術の基礎用…
​youtube​
磁性体中の電磁場を扱う場合、積分形は磁化電流と伝導電流を区別して考える際に有用です。磁場の強さHを導入することで、磁性体内部でも積分形が簡潔に表現できます。

 

参考）https://kabuto.phys.sci.osaka-u.ac.jp/~tanaka/emIIge/2008/section3_5.pdf
​

マクスウェル方程式積分形を使った計算手法

積分形を用いた実際の計算では、まず問題の対称性を見極めることが重要です。球対称、円筒対称、平面対称などの場合、積分経路や積分面を適切に選ぶことで線積分や面積分が簡略化されます。
​
例えば半径rの円形ループ中心を電流Jが貫く場合、円周上の磁場は一定となり、線積分は「磁場の大きさ×ループの長さ」に簡略化されます。この結果、磁場の強さは H(r) = J/(2πr) と求まります。このように平易な状況では、積分形は複雑な微分方程式を解くことなく結果を得られる利点があります。
​
一方で任意形状の導体や複雑な境界条件を持つ問題では、微分形を用いた数値解析が必要になります。有限要素法などの数値計算手法は微分形のマクスウェル方程式に基づいて開発されています。

 

参考）http://arxiv.org/pdf/2212.11930.pdf
​

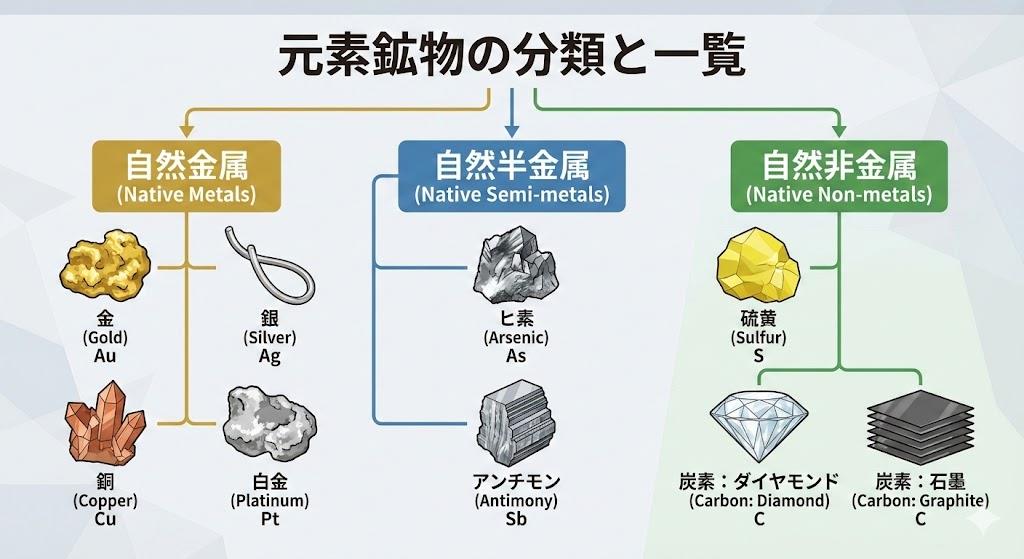
鉱石の磁気特性とマクスウェル方程式積分形

鉱石の持つ磁気的性質を理解する上で、マクスウェル方程式の積分形は基礎的な役割を果たします。磁性を持つ鉱石内部では、原子レベルの磁気モーメントが配列することで巨視的な磁化が生じます。この磁化の影響を記述する際、積分形は磁化電流と外部電流を統一的に扱う枠組みを提供します。
​
鉱石が外部磁場にさらされた際の応答を調べるには、磁場の強さHと磁束密度Bの関係式を積分形で表現します。磁性体中では H = B/μ₀ - M の関係があり、磁化Mの寄与を考慮する必要があります。閉曲線に沿ったHの循環を計算することで、磁性体内部の電流分布が分かります。
​
特に強磁性鉱石では、外部磁場を取り去っても残留磁化が残る現象があります。この挙動は積分形のマクスウェル方程式と物質固有の磁気特性を組み合わせることで記述できます。鉱物学や地球物理学において、岩石の磁化の歴史を読み解く古地磁気研究では、こうした積分形の理解が不可欠です。
​

 

 

マクスウェル方程式　電磁気学がわかる４つの法則