六角柱の面の数と頂点・辺の計算・結晶構造

六角柱の面の数と構造

六角柱は底面が六角形の角柱で、面の数は全部で8面です。底面が2つ（上面と下面）、そして側面が6つの長方形で構成されています。この構造は角柱の基本的な特徴を示しており、六角形の形状がそのまま立体の性質を決定づけています。

 

参考）作成中]中学受験】円/角柱の体積・展開図・表面積など分かりや…
​
角柱の面の数を求める公式は「n＋2」で表されます。六角柱の場合、底面の形が六角形なので n=6 となり、6＋2=8面という計算になります。この公式を使えば、三角柱（3＋2=5面）や五角柱（5＋2=7面）など、どんな角柱でも面の数をすぐに求められます。

 

参考）http://sirius.la.coocan.jp/sansu/6/rittai03.htm
​
底面と側面の関係を理解することで、立体の構造がより明確になります。六角柱では底面が正六角形の場合、すべての側面が合同な長方形になり、非常に規則的な形状となります。この対称性は自然界の鉱物結晶にもよく見られる特徴です。

 

参考）六角柱＝水晶が“柱のかたち”になる理由 ✨結晶構造から読み解…
​

六角柱の頂点の数え方

 

六角柱の頂点は12個あります。この数は底面の頂点数を2倍することで簡単に求められます。六角形の底面にはそれぞれ6個の頂点があり、上下2つの底面があるため、6×2=12個となります。

 

参考）角柱の頂点・辺・面の関係
​youtube​
n角柱の頂点数を求める一般的な公式は「n×2」です。これは角柱が常に2つの同じ形の底面を持つという性質から導かれます。三角柱なら6個（3×2）、四角柱なら8個（4×2）、五角柱なら10個（5×2）という具合に、底面の形によって頂点の数が決まります。

 

参考）https://www.adachi.ed.jp/adaoba-j/pdf/hibinoyubuyaki/12anser.pdf
​youtube​
頂点は立体図形の重要な構成要素であり、展開図を描く際や体積を計算する際の基準点となります。六角柱の12個の頂点は、すべて底面の六角形の角に位置しており、立体の骨格を形成しています。

 

参考）https://help.loilonote.app/%E5%B0%8F%EF%BC%95%E3%80%80%E7%AE%97%E6%95%B0%E3%80%80%E8%A7%92%E6%9F%B1%E3%82%84%E5%86%86%E6%9F%B1%E3%82%92%E3%81%A4%E3%81%8F%E3%82%8D%E3%81%86%E3%80%80%E8%A7%92%E6%9F%B1%E3%81%A8%E5%86%86%E6%9F%B1%E3%80%90%E6%8E%88%E6%A5%AD%E6%A1%88%E3%80%91%E4%B8%96%E7%94%B0%E8%B0%B7%E5%8C%BA%E7%AB%8B%E7%B5%8C%E5%A0%82%E5%B0%8F%E5%AD%A6%E6%A0%A1%E3%80%80%E9%9D%92%E6%9C%A8%20%E6%98%8E%E6%97%A5%E9%A6%99-664a87833965a7001d14bcad
​

六角柱の辺の本数と計算式

六角柱の辺は全部で18本あります。辺の数は「底面に12本（上下各6本）＋側面の縦の辺6本」という構成になっています。この計算方法を理解すると、展開図を描く際にも役立ちます。

 

参考）六角柱の辺の本数を答えなさい。 - の問題の求め方をおしえて…
​
n角柱の辺の数を求める公式は「n×3」です。六角柱の場合、6×3=18本となります。この公式の背景には、底面2つにそれぞれn本ずつの辺があり、さらに側面を形成する縦の辺がn本あるという構造があります。

 

参考）https://www.city.niiza.lg.jp/uploaded/attachment/15585.pdf
​
辺の数を理解することは、展開図を作成する際に特に重要です。展開図を作るには「面の数－1」本の辺を残して切り開く必要があります。六角柱の場合、8－1=7本の辺を残し、残りの11本を切ることで平面に展開できます。

 

参考）N角柱、N角すいの展開図の作り方｜中学受験プロ講師ブログ
​

オイラーの多面体定理と六角柱

オイラーの多面体定理は「頂点の数＋面の数－辺の数=2」という関係式で表されます。この定理は凸多面体のすべてに成り立つ普遍的な法則です。六角柱に当てはめると、12（頂点）＋8（面）－18（辺）=2となり、定理が成立することが確認できます。

 

参考）オイラーの多面体定理を解説！簡単な証明付きで即理解！｜高校生…
​
この定理は18世紀の数学者レオンハルト・オイラーによって発見されました。オイラーは数学の様々な分野で業績を残した天才で、複素数の指数関数「e^(iπ)=-1」という美しい公式でも知られています。多面体定理もまた、立体図形の本質を捉えた数学的に美しい関係式です。

 

参考）オイラーの多面体定理の意味と証明
​
n角柱では一般的に「2n＋(n＋2)－3n=2」が成立します。この式を展開すると、2n＋n＋2－3n=2、つまり2=2となり、どんな角柱でも必ずこの定理を満たすことがわかります。この普遍性がオイラーの多面体定理の魅力の一つです。
​
オイラーの多面体定理の詳しい証明と正多面体が5種類しか存在しない理由の解説

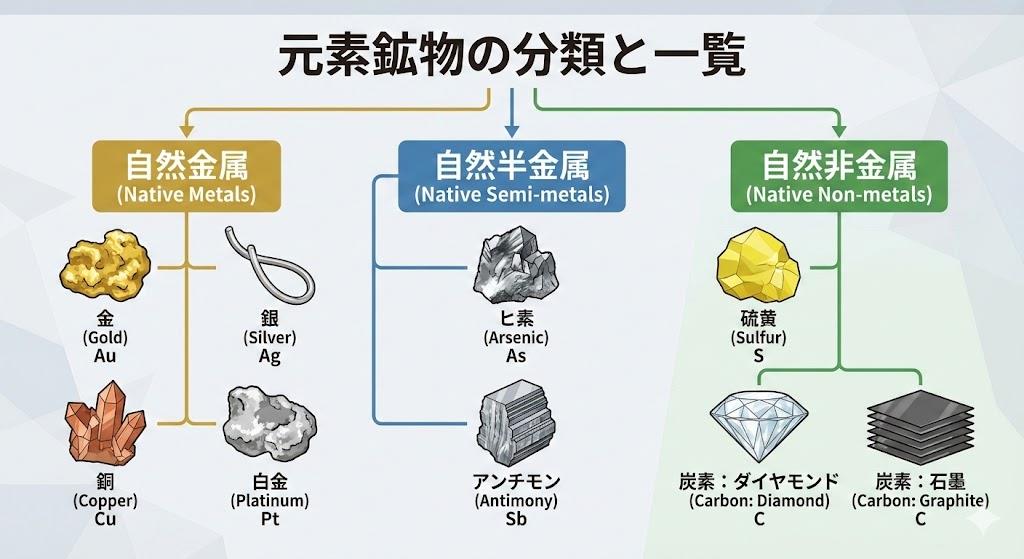
六角柱の結晶構造と鉱物

💎 水晶（石英）は自然界で最も有名な六角柱状の鉱物です。水晶は二酸化ケイ素（SiO₂）が規則正しく配列してできており、その分子構造が六角形のパターンで安定するため、外見も六角柱の結晶になります。この形は偶然の産物ではなく、内部の原子配列が外側の形状を決定づけているのです。

 

参考）https://himalayannaturalcrystal.com/?mode=f9
​
水晶の結晶は石英質の岩の上で、端正な結晶面で囲まれた六角錐の頭を持つ六角柱として成長します。その成長速度は非常に遅く、100年にわずか1mm程度と言われています。長い年月をかけて少しずつ積み重なることで、美しい六角柱の形状が完成します。
​
六方最密構造（HCP構造）も六角柱で表現される結晶構造です。この構造では正六角柱の上面・底面の各角と中心、そして高さ1/2の位置に3つの原子が配置されます。底面中心の原子は周囲の12個の原子と接しており、最も密に原子が詰まった配置となっています。金属や一部の鉱物がこの構造を持ちます。

 

参考）六方最密構造（単位格子に含む原子数・配位数・高さ・充填率の求…
​
水晶が六角柱になる結晶構造の仕組みと天然石の性質についての詳細記事

六角柱の展開図と面の配置

📄 六角柱の展開図を描く際は、底面2つと側面6つの配置を考える必要があります。一般的な描き方は、横に6つの長方形（側面）を並べ、その上下に六角形（底面）を配置する方法です。側面の長方形は縦の長さが六角柱の高さ、横の長さが底面の一辺の長さと等しくなります。
youtube+1​​
展開図から立体を組み立てる際、どの辺とどの辺が接するかを理解することが重要です。六角柱の場合、側面の6つの長方形が環状に連結し、その両端に底面の六角形が接続される構造になります。この配置を正確に把握することで、複雑な立体でも展開図から立体をイメージできるようになります。
youtube​​
展開図を作成する際は「面の数－1」本の辺を残して切り開く必要があります。六角柱では8－1=7本の辺を残し、18－7=11本の辺を切断します。どの辺を切るかによって様々な形の展開図ができますが、組み立てると同じ六角柱になります。この多様性も展開図の面白さの一つです。
youtube​​

六角柱の体積計算と表面積

六角柱の体積は「底面積×高さ」で計算します。正六角形の底面の場合、一辺の長さをA、高さをhとすると、体積は「(3√3/2)×A²×h」という公式で求められます。この公式は正六角形の面積公式（(3√3/2)×A²）に高さを掛けたものです。
youtube​
参考）正六角柱の体積・表面積・質量の計算機
​
📊 表面積は「底面積×2＋側面積」で計算します。側面積は6つの長方形の面積の合計となり、正六角柱の場合は「6×A×h」です。したがって、全体の表面積は「2×(3√3/2)×A²＋6×A×h」、つまり「3√3×A²＋6Ah」となります。
​
密度がわかっている場合、体積から質量を計算することもできます。質量=密度×体積という関係式を使い、木材や金属など材質の密度を用いて六角柱の重さを求められます。建築や工業分野では、六角柱形状の部材の重量計算にこの方法が活用されています。

 

参考）https://gakusyu.shizuoka-c.ed.jp/science/sonota/ronnbunshu/h28/162097.pdf
​
正六角柱の体積・表面積・質量を計算できるツールと詳しい計算式の解説

六角柱と他の角柱の比較

角柱の種類	面の数	頂点の数	辺の数
三角柱	5面	6個	9本
四角柱	6面	8個	12本
五角柱	7面	10個	15本
六角柱	8面	12個	18本
八角柱	10面	16個	24本

角柱の種類によって構成要素の数は規則的に変化します。底面の辺の数をnとすると、面の数は「n＋2」、頂点の数は「n×2」、辺の数は「n×3」という公式が常に成立します。この法則性を理解すれば、どんな角柱でも構成要素の数を暗算で求められます。

 

参考）https://www.min-san.com/pd/z5/41/1/kai/
​youtube​
🔺 角錐（ピラミッド型）との違いも重要です。n角錐の場合、面の数は「n＋1」、頂点の数は「n＋1」、辺の数は「n×2」となります。角柱と比較すると、角錐は底面が1つしかなく頂点が1つ追加されるため、構成要素の数が異なります。六角錐の場合、面は7面、頂点は7個、辺は12本です。

 

参考）空間図形の問題なんですけど、六角柱と七角錐の辺の数と頂点の数…
​
四角柱の中でも特に直方体や立方体は日常生活でよく見かける形状です。六角柱は四角柱よりも面や頂点が多く、より複雑な構造を持ちますが、その対称性の高さから自然界の結晶や建築物のデザインに利用されています。ハチの巣の六角形構造も、空間効率と強度の観点から六角形が最適な形状であることを示しています。
​

六角柱の構造強度と実用例

🏗️ 六角柱は構造的な強度に優れた形状です。同じ材料で作った場合、四角柱と比較すると接着面の長さや配置によって強度特性が異なります。辺が少ない四角柱の方が一辺の長さが長くなり接着面が大きくなる一方、六角柱は面の数が多く分散した力の伝達に有利な場合があります。
​
鉱物学では六角柱構造は非常に重要です。水晶以外にも、ベリル（エメラルドやアクアマリンの原石）、アパタイト、方解石の一部など、多くの鉱物が六角柱状の結晶として産出します。これらの鉱物は内部の原子配列が六方晶系に属するため、外見も六角柱になるのです。

 

参考）六方最密充填構造 - Wikipedia
​
化学や材料科学の分野では、六角柱構造は分子レベルでも重要な役割を果たします。六方最密構造は金属材料の基本的な結晶構造の一つで、マグネシウム、亜鉛、チタンなどの金属がこの構造を持ちます。この構造は原子が最も密に詰まった配置の一つで、材料の機械的性質に大きく影響します。

 

参考）【高校化学】「六方最密構造と単位格子」
​

 

 

[TANAKA・YA] 天然水晶 水晶 ポイント 六角柱 厳選 上品水晶原石 約4.5-6.5mm 置き物 シトリン ローズクォーツ 本水晶 アメジスト黄水晶 水晶原石 浄化用 鉱石 標本 観賞用 風水 癒し浄化 開運 お守り飾り用 紫水晶 ホーム装飾石 グッズ クリスマス 新年 プレゼント ヒーリング サンキャッチャー置物インテリア (本水晶)