磁気モーメント求め方を化学視点で解説｜不対電子数計算から鉱石磁性測定応用まで

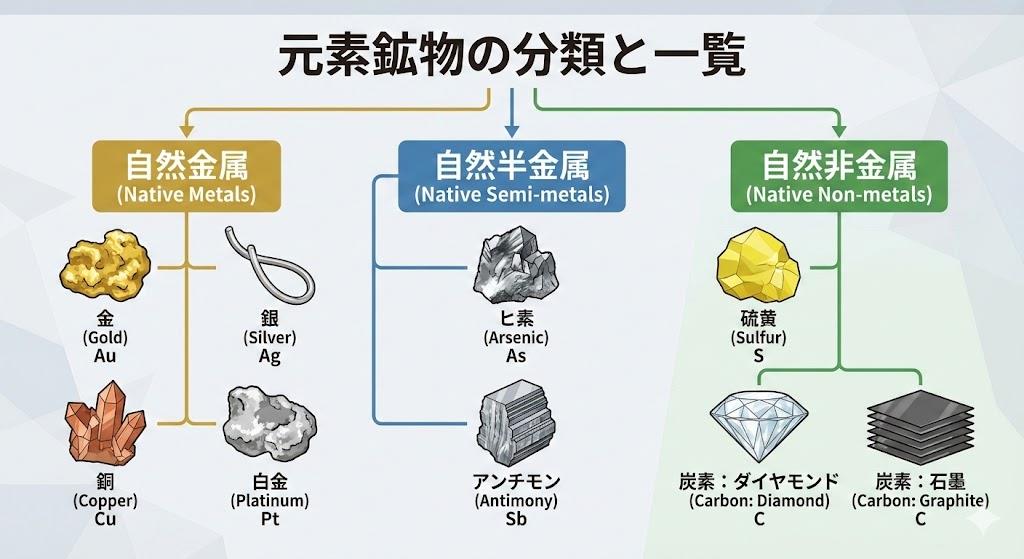
磁気モーメント求め方を化学で理解する

磁気モーメント求め方の基礎｜不対電子数とスピン角運動量の関係

化学における磁気モーメントは、原子や分子内の不対電子が生み出す磁気的性質を定量化する重要な物理量です。磁気モーメントの大きさを求めるには、まず物質中の不対電子の数を正確に把握する必要があります。

 

参考）スピンオンリーの式で磁気モーメントを求めよう【無機化学・錯体…
​
不対電子とは、電子軌道において対（ペア）を作らずに単独で存在する電子のことを指します。通常、電子は上向きスピン（↑）と下向きスピン（↓）がペアになることで磁気的性質を打ち消し合いますが、不対電子ではこの相殺が起こらず、磁気モーメントが発生します。

 

参考）Q05. 電子スピンとは？ 磁気モーメントとは？ 不対電子と…
​
電子のスピン角運動量は、量子力学的にℏ/2（ℏは換算プランク定数）の値を持ちます。このスピン角運動量が磁気モーメントの源泉となり、電子の回転運動による環状電流が周囲に磁場を発生させる仕組みです。不対電子数をn個とすると、全スピン角運動量Sは S = n × (1/2) と表現できます。

 

参考）遷移金属錯体の結晶場理論②【有効磁気モーメント/常磁性・反磁…
​

磁気モーメント計算式｜スピンオンリー式の導出と適用条件

遷移金属イオンの磁気モーメントを推定する最も基本的な方法が「スピンオンリー式」です。この式は以下のように表されます：​
μ = √(n(n+2)) [B.M.]
ここで、nは不対電子の数、B.M.はボーア磁子（Bohr Magneton）という磁気モーメントの単位です。ボーア磁子は μB = 9.27×10⁻²⁴ JT⁻¹ という値を持ち、電子の磁気モーメントを表す自然な単位となっています。

 

参考）ボーア磁子 - Wikipedia
​
スピンオンリー式が有効なのは、主に第一遷移金属系列（3d電子系）の錯体です。これらの錯体では、電子の軌道角運動量の寄与が比較的小さく、スピン角運動量のみを考慮すれば良い近似が成り立ちます。

 

参考）有効磁気モーメント
​
具体例として、3d電子数が5つの高スピン八面体型錯体を考えてみましょう。高スピン状態では、5つの電子がすべて同じ向きのスピンを持つため、不対電子数n=5となります。この値をスピンオンリー式に代入すると：​
μ = √(5(5+2)) = √35 ≒ 5.92 B.M.
このように、不対電子数から直接的に磁気モーメントを計算できます。
​

不対電子数	磁気モーメント（B.M.）
1	1.73
2	2.83
3	3.87
4	4.90
5	5.92

磁気モーメント実験測定法｜磁気天秤と磁化率から求める手法

理論計算だけでなく、実験的に磁気モーメントを測定する方法も化学研究において重要です。最も一般的な実験手法の一つが、磁気天秤（マグネティックバランス）を用いた測定です。

 

参考）ビデオ: エバンス法:不対電子と磁化率の計算
​
磁気天秤の測定原理は、不均一な磁場中に置かれた磁性体が受ける並進力 F = Mx・∂Hx/∂y を計測することで、磁気モーメントMを求めるというものです。この並進力の計測には、高感度の石英スプリング（約7cm/grの感度）が用いられ、その伸びから磁気力を測定します。

 

参考）磁気天秤 - Core Shool Paleomag 201…
​
磁気モーメントは磁化率χから以下の関係式で求めることができます：​
μ = √(3kχT/Nμ²B)
ここで、kはボルツマン定数、Tは絶対温度、Nはアボガドロ数です。この式を用いることで、測定した磁化率から磁気モーメントを算出し、さらに不対電子の数を逆算することが可能になります。
​
実際の測定では、Evans法と呼ばれるNMRを用いた磁化率測定法も広く利用されています。この手法では、試料溶液のNMRシグナルのシフトから磁化率を求め、磁気モーメントを計算します。得られた磁気モーメントの実測値を、スピンオンリー式から予測される理論値と比較することで、錯体の電子状態や結合性質を解析できます。
​

磁気モーメント求め方における全角運動量とランデg因子の役割

より精密な磁気モーメントの計算には、スピン角運動量だけでなく軌道角運動量も考慮する必要があります。特に重い原子や第二・第三遷移金属系列では、軌道角運動量の寄与が無視できなくなります。

 

参考）磁気モーメント - Wikipedia
​
原子の全角運動量Jは、軌道角運動量Lとスピン角運動量Sのベクトル和として定義されます：​
J = L + S
この全角運動量を用いた磁気モーメントの表式は以下のようになります：​
mAtom = gJ・μB・√(J(J+1))
ここでgJは「ランデのg因子」と呼ばれる重要なパラメータです。ランデのg因子は1921年にアルフレット・ランデがゼーマン効果の研究で導入したもので、以下の式で計算されます：
参考）ランデのg因子 - Wikipedia
​
gJ = 1 + [J(J+1) - L(L+1) + S(S+1)] / [2J(J+1)]
この因子により、軌道角運動量とスピン角運動量の異なる寄与を正確に考慮した磁気モーメントの計算が可能になります。純粋な軌道運動の場合はgJ=1、純粋なスピンの場合はgJ≒2となり、実際の原子ではこの中間の値を取ります。

 

参考）【多電子原子の磁性】全角運動量／ランデg因子／フント則
​
磁場中でのエネルギー変化は、ゼーマン効果として観測され、その大きさはランデのg因子を用いて以下のように表されます：​
ΔE = gJ・μB・H・M
ここでHは外部磁場、Mは全角運動量の磁場方向成分（磁気量子数）です。この関係式は、原子スペクトルの解析や磁気共鳴実験において不可欠な理論的基盤となっています。
​

磁気モーメント求め方の応用｜鉱石磁性評価と遷移金属錯体解析

磁気モーメントの測定と計算は、鉱物学や材料科学において重要な分析手法として活用されています。特に磁硫鉄鉱などの天然産鉱石の磁気的性質の評価では、磁気モーメント測定が不可欠です。

 

参考）https://www.gsj.jp/data/bull-gsj/07-03_04.pdf
​
鉱石の磁気モーメントを求める際には、外部磁場を変化させながら試料の磁化を測定します。磁硫鉄鉱の場合、室温から約300℃のキュリー温度まで加熱しながら磁気モーメントの変化を追跡することで、その磁性の起源や安定性を評価できます。実験では、外部磁場H=5000 Oe程度の条件下で石英スプリングの伸びを測定し、磁気力から磁気モーメントを算出します。
​
磁硫鉄鉱は反強磁性と常磁性の複雑な磁気構造を持ち、結晶方向によって磁性が異なる異方性を示します。六方晶系の結晶構造において、軸方向では常磁性を示すのに対し、底面方向では強い磁性を持ち、容易磁化方向が60°の周期を持つという特異な性質があります。
​
遷移金属錯体の解析では、測定した磁気モーメントから高スピン・低スピン状態を判別できます。例えば、d⁹電子配置のCu²⁺錯体（CuSO₄・5H₂O）では不対電子数n=1となり、計算される磁気モーメントは1.73 B.M.です。一方、d³電子配置のCr³⁺錯体では不対電子数n=3で、磁気モーメントは3.87 B.M.となります。
​
実測値と理論値の比較により、配位子場の強さや結晶場分裂のエネルギーを推定できます。高スピン錯体では測定値が理論値に近い値を示すのに対し、低スピン錯体では不対電子数が減少するため、磁気モーメントが小さくなります。この特性を利用して、錯体の電子状態や化学結合の性質を詳細に分析できます。
​
岩石鉱物鉱床学会誌
鉱石の磁気モーメント測定と岩石磁気の鉱床学への応用について詳細に解説された学術論文。磁硫鉄鉱などの天然鉱物の磁気的性質の測定方法と解析事例が豊富に記載されています。

 

理化学研究所プレスリリース
ダブルペニングトラップ法を用いた陽子の磁気モーメントの超高精度測定に関する研究成果。磁気モーメントの直接測定技術の最前線を知ることができる参考資料です。